The Logarithmic Function

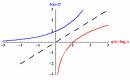
Previously we were graphing exponential equations in all bases (including base e), and in our assignment we graphed the reflections of these functions in the line y=x (the inverse functions...right?)

Those inverse functions you graphed are called Logarithms. Logarithms are exponents and will be manipulated with the same rules as any other exponents (to be discussed later). Lets take a look at how a logarithmic function is written.

An exponential function can be written as:



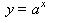
So exchanging the x and y coordinates produces yesterday's inverses, which can be written like:



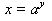
Or in logarithmic form the above looks like:



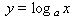
For this lesson we will concern ourselves with developing skill in sketching these functions. Look for similarities and differences between these and their exponential cousins (inverses). Tomorrow we will do some converting between the exponential and logarithmic forms of these functions.

A "Special" Exponential Function

This link (purplemath comes through yet again) describes what the "base e" is without going into too much mathematical "hocus pocus". Understanding this will help later on when you're answering questions and wondering what "continuous" meant in a mathematical sense.

(I'll wait here while you read the linked site)


So hopefully you're ready to graph some equations using the base e now...take a look at example 1 in your module and give it a try.

When you get to your assignment (specifically question #2) try to remember that to sketch an inverse of a function (not the reciprocal) you reflect the function in the line y=x. When the assignment moves on to talking about geometric series I suggest you read question 5 first.

Exponential Equations

The link above will take you to the Pre-Calculus site on Logarithms. Logaritms is a tool we use to solve exponential equations. As with all of our other studies, we will begin with graphing exponential equations, then we will move to solving them for particular values.

Graphing an exponential equation will be just like graphing any other equation we have studied so far. You can start with a table of values. Eventually we will notice some patterns and be able to graph by inspection of the equation. Let's start with a few characteristics of all exponential equations.

1.They pass through the point (0,1).
2.D: {all real numbers}
3.R: (0, ∞)
4.They have y=0 as an asymptote.

Of course we can apply other translations to exponential functions just as we have with every other function we have studied. I strongly recommend completing example 2 in the module to get a feel for the other types of translations.

Once we have developed some comfort with these equations we will begin to solve for x. We have already seen this type of question (take a look at example 1) by finding a common base. Try the following one if you like.



After we are familiar with exponential equations and their graphs we will solve equations that do not have a common base.